前面兩篇文章跟大家解釋了局的基本概念。 有網友在文末留言問到:「有沒有甚麼科學性的方法能協助我們分析局呢? 讓這整件事情不只是籠統的感覺。」
有,賽局理論的很多技術就是為了解決模糊性而產生的。 其中一個最入門的東西,就是「效用分析」這樣的概念。
效用分析指的是我們在一個局勢中,把雙方(或多方)手上的牌以及彼此可能的出牌法做個整理,並盡量去推敲每種出牌法對於雙方可能產生的價值。 把各選項的價值列出來後,更可以據此判斷最可能有交集之處。
不過,特別要說明的是,局勢分析時「價值」其實不是我們慣用的字眼,通常是用「效用」兩字。 原因在於「價值」通常是個絕對值,並可以客觀衡量或比較的,比方說金額、勞務量、或是時間。 可是人做某個決策未必完全是以絕對價值做評估;讓心情輕鬆、被人感謝、友情、快樂度、或是良善可能對當事人而言也很重要。 對某些人而言,玩得愉快有可能比多賺一塊錢效用更高。 所以我們一般做分析時,指的是某個選擇對當事人而言的整體效用,而非單指金錢價值。
一般這類分析,我們可能透過樹狀圖(extensive form) 或矩陣圖(normal form) 來作呈現。 樹狀圖的部分我們可以之後再來談,若急著想看的讀者,其實在我之前的文章中曾經用過幾次。 比方說所謂浪漫這件事情這篇文章後段的分析方式就是典型以樹狀圖攤開整個局勢的做法。
而矩陣圖的分析方式,常見於賽局理論的書籍中。 會把雙方的選擇以表單的方式做成所謂的償付矩陣(pay-off table)。 其中分別列出雙方在各選擇中,各自效用的相對分數。
一個典型償付矩陣的圖形類似下圖:
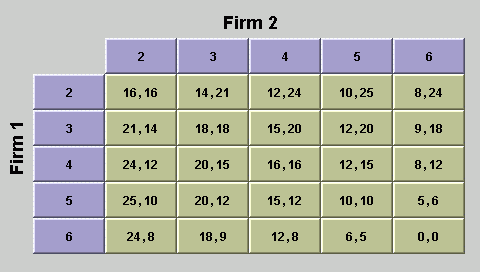
那當然,對很多人而言這圖可能很複雜。 所以繼續用上次那個小秘書的範例來做解說好了。 (忘記的朋友可以點此 賽局基礎 之 小秘書的選擇 去回憶一下)
延續上篇的內容,你需要人家幫你。 老闆說可以去找他的秘書Cindy幫忙。 可是Cindy在那個下午,原本其實是沒事的。 所以她可能有兩個打算:
A. 繼續玩Facebook
B. 幫你整理名單
你則也可以有兩個打算:
A. 等她幫忙
B. 不等她直接做
當然,雙方實際上的選擇可能還多很多,但為了讓情境說明簡單,我們就假設兩方各只有兩個選擇。
因為選項各只有兩個,所以我們可以先畫出一個3*3的方格。 (如下圖)

圖畫好後,在最上面一列,可以先寫出自己的兩個選項;在最左邊的一行,則寫下小秘書的兩個選項。

做這類效用分析時,我一般先考慮Y軸角色的選擇。 並把認知的效用數值填在格子中。
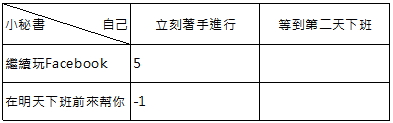
為何是5與-1? 這兩個數值代表甚麼具體的涵義呢? 5跟-1的數值,僅是「根據我對小秘書性格認知」所做的推估。 數值本身只是一個「相對分數」。
以我對她的認知而言,一個不用做事的下午對她可能很重要,能整個下午上網她會很開心,所以我暫且把這選項的分數訂為5。 至於整理名單,照前文的描述,很難帶給她甚麼回報。 自己只是個新進的業務,既不能決定她的薪資、也不能給她獎金、也不是公司有地位的人,所以她來幫自己,實在沒有具體的收益。 或許為善最樂是一個效用,可是我跟她並不熟,所以不清楚她是否會因為助人而快樂。 暫且假設她非常效益導向→ 做任何沒有回報的事情效用會是負的,所以就先給予一個-1的分數。
要強調的是,我對她的假設有可能是錯的。 所以在實務中,當你有更多資訊後,有可能需要回頭修正這個償付矩陣。 修正後,判斷也可能隨之改變。 但第一步,我們可以先悲觀一些,所以5以及-1的分數就先這麼定吧~。
再來,我需要評估一下自己兩個選項的可能報酬。
1. 如果我不等她來幫忙,立刻開始著手進行。 雖然會辛苦一些,可是可以即時做完,不會砸鍋、不會被罵、可以順利交差;但相較於別人可以開心玩一下午而言,我這選項實在稱不上多完美。 所以我給一個相對分數3分。
2. 若我立刻開始著手進行,做了一大半時她居然也來幫忙了。 雖然她的後續加入對我幫助沒這麼大,但最少減輕了我的部分壓力。 所以我的效用價值會稍微提升,那給個4分的分數並不為過。
3. 反過來說,若我只是痴痴的等她來幫忙,結果她是唬弄我,只是一直待在座位上玩Facebook。 那等到第二天下班後(可以看前篇的假設),我會做不完工作。 這時候自己不但會被挨罵、搞不好還被開除了。 若事情演變成這樣,那我的效用最糟糕,所以對這選項給一個-1的分數。
4. 至於若我痴痴的等,她即時來幫忙並擔負了大部分的工作,那我就能如期把工作做完。 可是「不知道她是否會出現」的那種恐怖心情,其實是很折磨人的。 所以折算起來,我覺得對我的效用也只有3而已。
所以若把四個可能結果的效用分數都放入矩陣圖,一個完整的償付矩陣就出現了
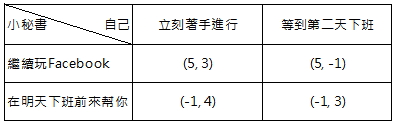
這張圖還有幾個重點要說一下。
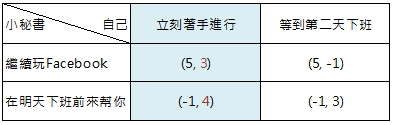
首先,我們若把小秘書的兩個選項中,效用值最大的那一列標註起來。 你會發現玩Facebook相較於在明天下班前來幫忙的報酬要來的高。 (也就是下表綠色那一列)
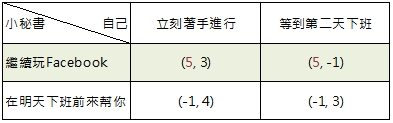
再來,不管自己選擇哪個方案,對小秘書而言,她這選項的效用都最高。 這也就是前一篇稱之為「優勢策略」(Dominant Strategy)的東西。
優勢策略的意思就是:無論對方打算怎麼反應,自己做那選項都能確保效用最大化。
那我對而言,把直向選擇中,數值最大的那一欄找出來,也會是相對選項較高的一條選擇途徑。
(另外,網友小汀也在留言補充道:當自己沒有優勢策略, 但對手有時, 就假設對手會使用優勢策略, 然後根據他的策略選擇自己的最佳反應。 這是另一個判斷的方式,在此補充。)
換言之,不論她會不會幫忙,我若都選擇在第一時間開始著手進行,那我能最大化報酬。 所以立刻開始著手進行,這會是我的優勢策略!
再來,若我們把兩人的優勢策略都Highlight出來,會發現有個交集點,也就是下圖的深藍色那一格。
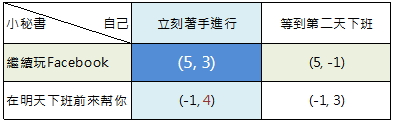
這個格子就是在前文中所提到「組力最小的路」。 照賽局理論的術語而言,這點也就是所謂「納許均衡」(Nash Equilibrium)。
納許均衡在學理上的定義,指的是賽局中所有參與者都自認為下了最佳決策的匯集處。 在整個賽局規則不改變的情況下,參與者不會再任意改變選項。 不過要提醒的是,納許均衡未必是整個賽局的最佳解,只代表這賽局最後各方選項的交集處。 這也是為何會有所謂囚徒困境的案例。因為在囚徒困境的賽局中,大家雖然各自選擇了一個對自己最有利的選擇,可是當把局勢合在一起而言,那個選擇卻會導致雙輸。
所以學賽局理論的一個重點,就是看清楚壓力最小的點在哪裡;那個點到底對參與者有利,還是不利。 比方說,如果自己是小秘書,那可以順勢而為,不用改變自己,反正對方無論怎麼選擇,自己都能以逸待勞。 可是如果自己是需要幫忙的那個人,那你知道整個局勢是對自己不利的。 要不就是坦然接受不利的狀況,自己立刻著手工作;不然就是想辦法扭轉賽局,以促成其中成員間的合作。
比方說如果我日後升職且有權限可以主導她的獎勵機制時,原本報酬矩陣的納許均衡就有機會打破。當獎勵增加到夠大時,她幫我的效用就可能變成正的。 像下圖就顯示了當獎勵對她的效用大於玩Facebook時,就有可能產生另一個新的納許均衡。 而當獎勵效用夠大時,就有可能誘發交集到右下角處。
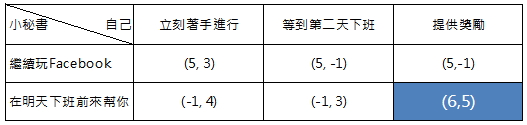
你透過改變局的規則而變動參與者的選擇方式;同樣的,也創造了一個雙贏的局面。
所以,重複一下上一篇的結論:學習局的知識,不是要你去權謀,而是要你看懂別人的需求,並把對抗轉成合作。
畢竟合作,才是讓事情順利的關鍵!
本站所有文章未經事先書面授權,請勿任意利用、引用、轉載。

























